跳转至

Logistic regression and GWAS

约 1117 个字 预计阅读时间 4 分钟

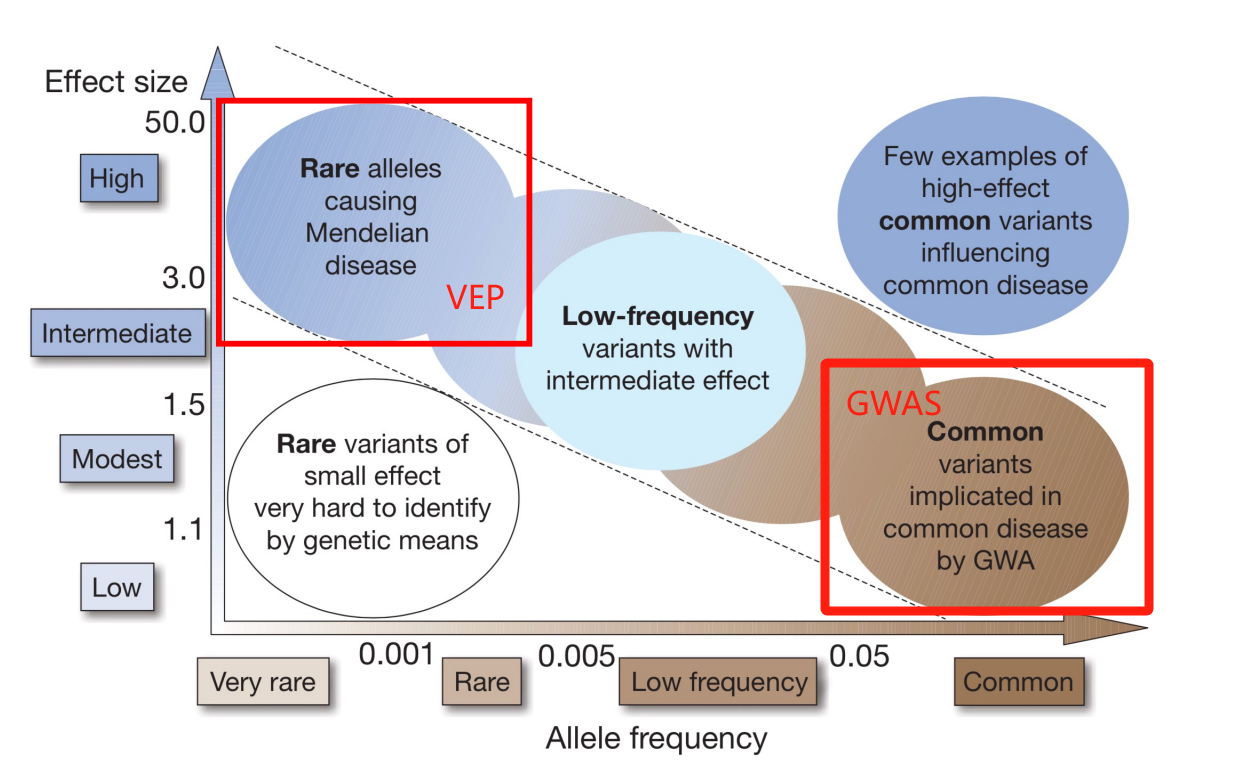
全基因组关联研究（GWAS，Genome-Wide Association Study），是一种病例-对照研究设计。研究选取很多人类个体，并分为患病组和未患病组。通过使用机器学习方法来比较两组个体的基因组数据，研究者可以找出可能与疾病相关的基因变异。GWAS 的目标是找到与疾病相关的常见基因变异，以此帮助理解疾病的遗传基础。

首先，研究者收集个体的基因序列信息。我们重点关注于单核苷酸多态性(Single nucleotide polymorphism, SNP)，即DNA序列中一个碱基对的变化对疾病表现型的影响。例如父母的某个位点上可能有一个碱基为C，但子代中可能会有一个变为T的变异位点。这个变异位点正是GWAS研究的重点。

由于每个个体都有23对染色体，因而所有受试者在 DNA 上有配对的等位基因，序列采集后会得到两组基本相同的序列（可能含有等位基因变异）。我们因此可以得到碱基变异的剂量(Dosage Information)。

  • 0剂量：个体的两条染色体上都是参考等位基因（0/0）。

  • 1剂量：一条染色体是参考等位基因，另一条是备选等位基因（0/1）。

  • 2剂量：两条染色体上都是备选等位基因（1/1）。

在实际研究中，基因变异的数据以VCF格式存储。VCF文件中包含了：

  • 染色体和位置信息（Chromosome & Position）

  • 参考等位基因（Ref）和备选等位基因（Alt）

  • 每个个体的基因型信息（Genotype），如0/1、1/1等，表示该位点上参考和备选等位基因的组合。

  • 该变异的注册ID编号（ID）。

alt text

Logistic Regression

接下来我们明确我们的任务目标。我们希望通过分析每个 SNP 与疾病发生的相关性，最终通过统计检验获得与疾病显著相关的 SNP。

在 GWAS 中，我们希望使用 Logistic 回归，来得到每一个变异剂量 \(X\) \((X=0,1,2)\) 对应的疾病的可能性 \(P(Y=1)\)。

Logistic 回归的目的是通过回归系数 \(\beta\) 来估计 SNP 剂量 \(X\) 与 疾病状态 \(Y\) 之间的关系。回归模型如下：

\[ \text{logit}(P(Y=1)) = \beta_0 + \beta_1 X \]

其中：

  • logit 函数：定义为 \(\text{logit}(p) = \ln \left( \frac{p}{1-p} \right)\)，是为了将概率 \(p\) 映射到实数范围来对应 \(\beta_0+\beta_1 X\)。

  • \(P(Y=1)\) 是个体患病的概率，即 \(Y = 1\) 的概率。

  • \(\beta_0\) 是截距。

  • \(\beta_1\) 是自变量 X 的回归系数。

我们希望通过已知的 X 和 Y 来估计 \(\beta_0\) 和 \(\beta_1\)。

解出这个方程，我们可以得到：

\[ P(Y=1) = \frac{1}{1 + e^{-(\beta_0 + \beta_1 X)}} \]

这就是 Logistic 回归的核心公式，通过这个公式我们可以预测某个个体的患病概率 \(P(Y=1)\)，其输入是 SNP 剂量信息 X。

为了得到 \(\beta_0\) 和 \(\beta_1\)，我们使用极大似然估计法（Maximum Likelihood Estimation, MLE）。MLE 的目标是找到让整体观测数据 \((X, Y)\) 的可能性最大的 \(\beta_0\) 和 \(\beta_1\)。

假设有 \(n\) 个个体的数据。对于每个个体 \(i\)，观测值 \(Y_i\) 是 0 或 1，概率为 \(P(Y=1|X)\)，即：

\[ L(\beta_0, \beta_1) = \prod_{i=1}^{n} P(Y_i=1|X_i)^{Y_i} \cdot P(Y_i=0|X_i)^{1 - Y_i} \]

这个似然函数表示的是给定每个 \(X_i\) 值时，\(Y_i = 1\) 或 \(Y_i = 0\) 的概率。

为了简化计算，我们取对数得到对数似然函数：

\[ \ln L(\beta_0, \beta_1) = \sum_{i=1}^{n} \left[ Y_i \ln P(Y_i=1|X_i) + (1 - Y_i) \ln (1 - P(Y_i=1|X_i)) \right] \]

通过最大化对数似然函数，求解出 \(\beta_0\) 和 \(\beta_1\)。

我们接下来使用梯度下降法迭代求解最佳的 \(\beta_0\) 和 \(\beta_1\)。

\[ \beta_j \leftarrow \beta_j + \alpha \cdot \frac{\partial \ln L}{\partial \beta_j} \]

其中，\(\alpha\) 是学习率。

反复迭代，直到对数似然函数收敛，得到最优的 \(\beta_0\) 和 \(\beta_1\)。

一旦通过梯度下降法或其他优化算法求得了 \(\beta_0\) 和 \(\beta_1\)，我们就可以对模型进行解释：

  • \(\beta_1\) 是 SNP 剂量 \(X\) 对患病概率 \(P(Y=1)\) 的影响。如果 \(\beta_1 > 0\)，表示 SNP 剂量越高，患病的概率越高；如果 \(\beta_1 < 0\)，表示 SNP 剂量越高，患病的概率越低。

  • 使用估计得到的 \(\beta_0\) 和 \(\beta_1\) 可以计算每个个体的患病概率：

\[ P(Y=1|X) = \frac{1}{1 + e^{-(\beta_0 + \beta_1 X)}} \]

statistic analysis

通过上面的方法，我们得到了每一个 SNP 变异位点对应的疾病发生的概率。例如，当某个体出现第 \(i\) 个 SNP 变异位点，并通过这个模型计算出该个体在 SNP 位点上的剂量值 \(X_i\) 所对应的概率 \(P(Y=1∣X=i)=0.9\)，那么我们可以人为该个体有 90% 的概率患病。

然而，由于 GWAS 通常会对大量的 SNP 进行分析（通常上百万个），这就引入了一个问题，即我们可能会得到很多假阳性（false positives），这意味着我们错误地认为某些 SNP 与疾病有关，而实际上它们并没有关系。

因此我们需要来进行统计学分析，尝试降低这部分产生的假阳性，提高准确度。

在 GWAS 中，我们对每个 SNP 都会进行一个假设检验，假设原假设为 \(H_0: \beta_1 = 0\)（即该 SNP 对患病没有影响）。通过 Logistic 回归分析得到的回归系数 \(\hat{\beta}_1\) 和标准误差 \(SE(\hat{\beta}_1)\)，可以计算出 Z 值：

\[ Z = \frac{\hat{\beta}_1}{SE(\hat{\beta}_1)} \]

Z 值可以用来计算 P 值，它表示如果原假设为真（即该 SNP 对疾病没有影响），我们会观察到如此极端的检验统计量的概率。P 值越小，说明该 SNP 与疾病的关联越强。

2. 显著性阈值 \(\alpha\)：

为了判断一个 SNP 是否与疾病显著相关，通常会设定一个显著性水平（例如 \(\alpha = 0.05\)），这表示我们接受最多有 5% 的假阳性率。如果 P 值小于 \(\alpha\)，我们就可以拒绝原假设，认为该 SNP 与疾病有关。

然而，当我们在 GWAS 中分析大量的 SNP 时，这样的显著性水平会导致很多假阳性。假设我们测试了 1,000,000 个 SNP，如果每个 SNP 的显著性水平为 \(\alpha = 0.05\)，那么理论上会有 5% 的假阳性，也就是：

\[ 1,000,000 \times 0.05 = 50,000 \text{ 个假阳性} \]

这就意味着在 1 百万个变异位点中，我们可能会得到 50,000 个假阳性，即错误地认为 50,000 个 SNP 与疾病相关，而实际上它们并没有关联。

3. 多重假设检验校正：

为了控制假阳性率，GWAS 采用了多重检验校正方法。图片中提到了两种常见的校正方法：

  1. Bonferroni 校正：
  2. 这是最常用的一种校正方法，用来控制至少一个假阳性的出现概率。
  3. 它通过将显著性水平 \(\alpha\) 进行调整，除以测试的总数目 \(m\)，即新的显著性水平为：
\[ \alpha_{\text{new}} = \frac{\alpha}{m} \]
 例如，如果我们测试 1,000,000 个 SNP，并设定 $\alpha = 0.05$，那么 Bonferroni 校正后的显著性水平为：
\[ \alpha_{\text{new}} = \frac{0.05}{1,000,000} = 5 \times 10^{-8} \]

只有 P 值小于这个非常小的阈值时，我们才会认为该 SNP 与疾病有显著关联。

  1. Benjamini-Hochberg 校正（FDR 控制）：

这种方法控制的是错误发现率（False Discovery Rate，FDR），即我们发现的显著结果中有多少比例是假的。它是一种更宽松的校正方法，允许一定比例的假阳性，从而增加检测显著 SNP 的能力。FDR 控制的方法在 GWAS 中也广泛使用，尤其当我们不需要严格控制每一个 SNP 的假阳性，而是希望在假阳性率可控的情况下找到更多的关联位点时。

为什么我们更多的不希望有太多的假阳性？

假阳性结果会误导研究者，使他们去进一步研究那些实际上与疾病没有关联的 SNP，浪费时间和资源。

妈的，概率论没学好，先弃坑了。