傅里叶变换

约 593 个字 预计阅读时间 2 分钟

复数矩阵

复数向量操作

对复数向量 \(\begin{bmatrix} z_{1} \\ z_{2} \\ \vdots \\ z_{n} \end{bmatrix} \in C_n\)，定义 \(|z|^2=z^Hz=\bar z^Tz\)（先取共轭，再转置相乘）

同样，复数向量内积变为 \(yx=y^Hx=\bar y^Tx\)

复数矩阵操作

复对称矩阵定义为：若 \(\bar 𝐴^𝑇 = A\)，则 \(A\) 为对称阵。这样的矩阵我们称为埃尔米特矩阵，满足\(A^H=A\)。

酉矩阵（Unitary Matrix）有一组标准正交基，正交符合附属向量内积为 \(0\) 的特征。酉矩阵的性质为：\(Q^HQ=I\)

快速傅里叶变换（FFT）

将传统的矩阵乘法的时间复杂度 \(O(n^2)\) 降低到了 \(O(nlogn)\)

傅里叶矩阵

傅里叶矩阵\(F_n\)本身也是一个酉矩阵，给出傅里叶矩阵形式:

\[ F_n = \begin{bmatrix} 1 & 1 & 1 & \cdots & 1 \\ 1 & w & w^2 & \cdots & w^{n-1} \\ 1 & w^2 & w^4 & \cdots & w^{2(n-1)} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 1 & w^{n-1} & w^{2(n-1)} & \cdots & w^{(n-1)^2} \end{bmatrix} \]

(计数从 0 开始,到 n-1 结束)

其中\(w_n = 1\), \(w = e^{i2\pi/n} = \cos(2\pi/n) + i\sin(2\pi/n)\)

注:计算时不要用 \(a+bi\) 形式计算，应使用 \(e^{i2\pi/n}\) 计算。反映在复数坐标系上：

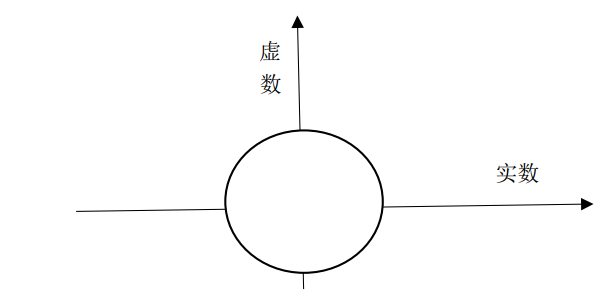
\(w = e^{i2\pi/n}\) 就反映在这个圆上，其中的 \(n\) 表示将这个圆分成几部分，分别为: \(w\), \(w^2\), \(w^3\) ......... \(w^n\)。

快速傅里叶变换

快速傅里叶变换主要就是因为 \(F\) 的不同乘方之间有所关联，因此我们可以对\(F\)进行分解。以\(F_{64}\)与\(F_{32}\)为例：

代入公式 \(w = e^{i2\pi/n}\) 可以看出来，\(F_{64}\)中的\(w_{64}\) (下标代表元素属于哪个矩阵) = \((w_{32})^2\)

构造矩阵转换:

\[ \begin{align*} \begin{bmatrix} F_{64} \end{bmatrix} = \begin{bmatrix} I & D \\ I & -D\end{bmatrix} \begin{bmatrix} F_{32} & 0 \\ 0 & F_{32} \end{bmatrix} \begin{bmatrix} P \end{bmatrix} \\\\ \end{align*} \]

其中，置换矩阵 \(P\) 的作用是将奇偶行分开，目的是减小计算量。而前面的 \(D\) 代表着对角矩阵。

例如 4 维时,置换矩阵 \(P = \begin{bmatrix} 1 & 0 & 0 & 0\\ 0 & 0 & 1 & 0\\ 0 & 1 & 0 & 0\\ 0 & 0 & 0 & 1 \end{bmatrix}\).

\(D\)矩阵则为 \(D = \begin{bmatrix} 1\\ w\\ w^2\\ \ldots\\ w^{31} \end{bmatrix}\),

而矩阵\(\begin{bmatrix} I & D \\ I & -D\end{bmatrix}\)的作用就是将\(F_{32}\)转化为\(F_{64}\)。

如果继续这样分解下去，一共进行\(log_264\)次分解。最后，只剩下了修正项的运算,\(F\) 变为 \(I\)。